Norges landbrukshøgskole Institutt for tekniske fag

Løsningsforslag til

eksamen i fag
TML300 Reguleringsteknikk

holdt 4. desember 2000 kl. 0900 – 1400 (5 timer)

1.  

   
   
   

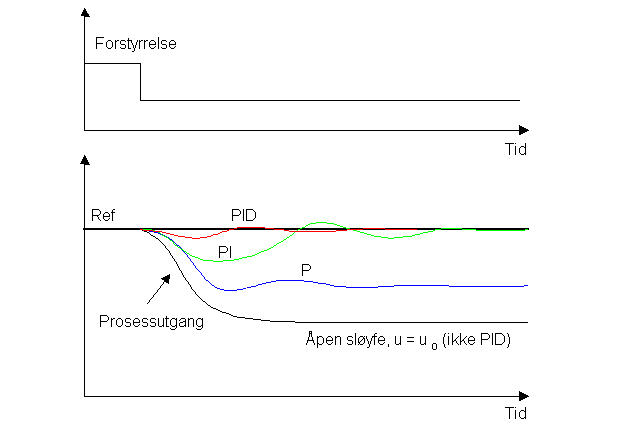
2. Struktur, se figuren nedenfor.

   

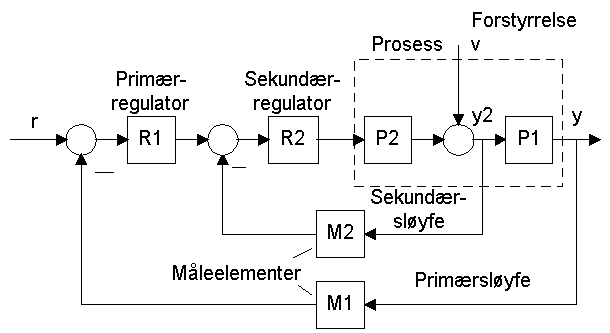
   Hensikt: Hurtig kompensering for forstyrrelsen (sammenliknet med enkeltsløyferegulering). Kan dessuten virke lineariserende på ulineære prosessdeler.

   Regulatorinnstilling: Først R2 med R1 i manuell. Så R1 med R2 i auto.

   Eksempel:

   Figuren nedenfor viser et instrumenteringsskjema for et temperaturreguleringssystem for en varmeveksler basert på kaskaderegulering.

   

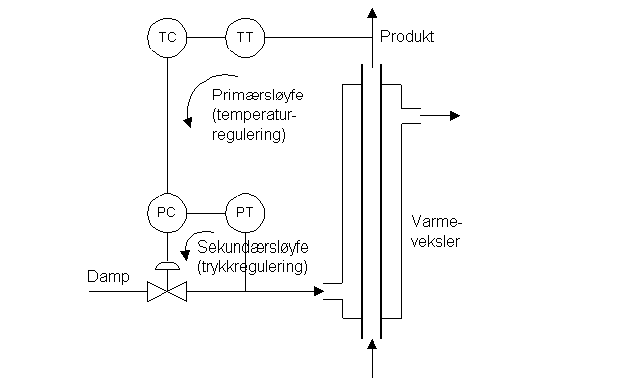
   Trykkreguleringssløyfen vil kompensere for trykkvariasjoner i damptilførselen. Dette vil medføre at effekttilførselen blir jevnere, dvs. mindre påvirket av trykkvariasjonene, og dette vil igjen medføre at temperaturen får et jevnere forløp

   
   
   

3. Kontinuerlig PI-regulator:

   u = K_pe + (K_p/T_i)integral(e)

   Deriverer:

   du/dt = K_pde/dt + (K_p/T_i)e

   Eulers bakovermetode: du/dt er tilnærmet lik [u(k)-u(k-1)]/T_s, og de/dt er tilnærmet lik [e(k)-e(k-1)]/T_s. Dette innsatt for de deriverte ovenfor gir (etter ordning av uttrykket):

   u(k) = u(k-1) + K_p[e(k) - e(k-1)] + (K_pT_s/T_i)e
   
   

4. PID-regulator:

   u(t)=u₀+u_p+u_i+u_d

   der

   u₀ er nominelt pådrag.

   u_p=K_p e er proporsjonalleddet. K_p er forsterkningen.

   u_i=(K_p/T_i) * (integralet av avviket e fra 0 til t) er integralleddet. T_i er integraltiden.

   u_d=K_pT_dde_f/dt er derivatleddet. T_d er derivattiden. 

   e_f lavpassfiltrert avvik gitt ved

   e_f(s) = [1/(T_fs + 1)]*e(s)

   der T_f er filtertiden.

   
   
   
5. Frekvensresponsen er

   h(jw)=K(T₁jw+1)*e^-Tjw/(T₂w+1)

   Ved å skrive telleren på polarform og nevneren på polarform, fås

   Amplitudefunksjonen=|h(jw)|=K×sqrt(T₁²w²+1)/sqrt(T₂²w²+1)

   Fasefunksjonen=arg[h(jw)]=arctan(T₁w) - arctan(T₂w) - Tw[rad]

    

 
6. Se figuren nedenfor (båndbredden er 10 rad/s).

   

7. Gitt følgende modell:

   dx₁/dt = 5*u₁ + x₂ + 4x₁  
   

   dx₂/dt = 2x₂ + 3x₁ + 7*u₂ + 8*u₁
   

   
   y = x₁ + 3x₂ + 9u₁

    
   1. Blokkdiagram:

      

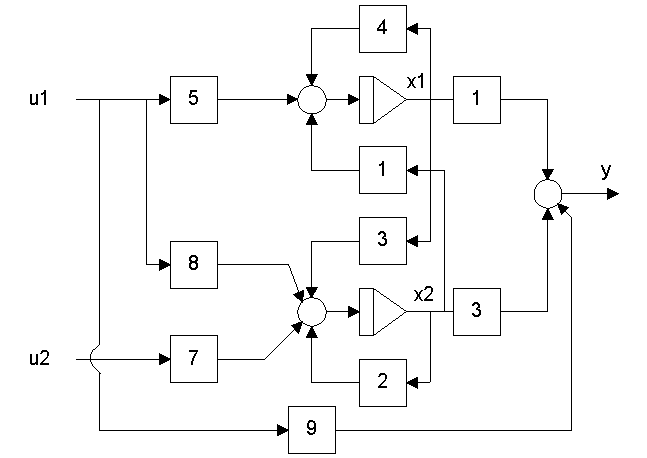
   2. dx₁/dt = 4x₁ + x₂ + 5u₁
      dx₂/dt = 3x₁ + 2x₂ + 8u₁ + 7u₂
      y = x₁ + 3x₂ + 9₁u
      

      eller

      dx/dt=Ax+Bu
      y=Cx+Du

      der (i Matlab-notasjon)

      x=[x₁; x₂]
      u=[u₁; u₂]
      y=y (skalar)

      A=[4, 1; 3, 2]
      B=[5, 0; 8, 7]
      C=[1, 3]
      D=[9, 0]

    
8.  
   1. sim simulerer et Simulink-blokkdiagram.
   2. ss lager en LTI-modell i form av en tilstandsrommodell.
   3. step simulerer sprangresponsen for en LTI-modell.
   
   
   
9. Energibalanse: 

   crVdT/dt = cw(T_i-T)  + U(T_o-T) + P

   Prosessen kan tegnes som i figur 2.10 i læreboka.

   
   
   

10.  
    1. (5) h(s) = Kw₀²/[s²+2zw₀s + w₀²]*e^-Ts
    2. (5) Responstiden T_r er 63%-stigetiden i sprangresponsen. For systemet ovenfor: T_r er tilnærmet (1,5/w₀) + T.
       
       
11. Prosessen skal først bringes til eller nær det nominelle arbeidspunktet ved å justere det nominelle pådraget. I tuningsfasen skal prosessen være regulert av en av/på-regulator med utgangsamplitude M, dvs. at pådragsbidraget fra av/på-regulatoren er +M eller -M. Det oppstår da stående svingninger i reguleringssløyfen. Amplituden i reguleringsavviket skal avleses og betegnes E. Periodetiden i svingningene avleses og betegnes T_k. Den kritiske forsterkningen K_pk beregnes som K_pk = 4M/(pE). (Ikke forventet svar, men tas med her: PID-parametrene beregnes så ihht. Ziegler-Nichols' lukket-sløyfe-metode: K_p=0,6·K_pk, ,  T_i=T_k/2, T_d=T_k/8 .)

    
    
    

12. Regulatoren innstilles i forskjellige arbeidspunkter (det forutsettes at prosessen har forskjellige dynamiske egenskaper i arbeidspunktene). Det antas at prosessdynamikken kan relateres eller identifiseres til en prosessvariabel P, f.eks. massestrøm gjennom en tank. Dette gir et sett verdier for Kp, for Ti og for Td. Regulatoren blir adaptiv ved at hver av regulatorparametrene beregnes med hver sin funksjon av P, dvs. Kp = f1(P), Ti=f2(P), Td=f3(P) basert på f.eks. lineær interpolering mellom verdiene i parametersettet. Kp, Ti og Td blir med dette varierende, og til en hver tid tilpasset prosessens dynamiske egenskaper, dvs. adaptiv.
    
    
13.  
    • Enkeltsløyferegulator. Enkel og rimelig løsning. Robust, siden reguleringen utføres av en dedikert mikroprosessor i regulatoren. Dårlig brukergrensesnitt (ingen skjerm med grafikk).
    • PLS-system. Nokså kostbar løsning. Modulært, dvs. kan bygge ut med flere moduler etter behov. Kan bruke programmeringsspråk som benyttes i industriell automatisering, men dette kan også være begrensende. Må ha tilleggsprogramvare for evt. grafisk brukergrensensitt (på PC). Robust, siden reguleringen utføres av en dedikert mikroprosessor i regulatoren.
    • PC-basert system. Rimeligere enn PLS. Svært fleksibelt mht. utforming av brukergrensesnitt og annen funksjonalitet ved bruk av f.eks. LabVIEW. Ikke så robust som de ovennevnte løsningene siden programutførelsen foregår på PC'ens mikroprosessor (men en kan anskaffe I/O-kort med innebygget mikroprosessor, og en kan laste ned programmet til denne og få programmet kjørt der).

Finn Haugen, faglærer.