Aliasing at Sampling

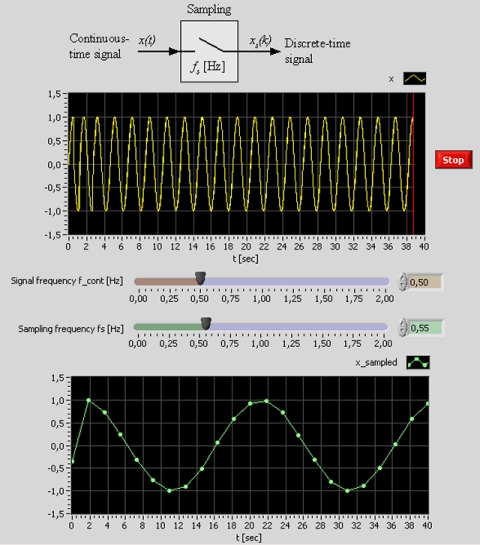
Snapshot of the front panel of the simulator:

• What is needed to run the the simulator? Read to get most recent information!
• Tips for using the simulator.
• The simulator: aliasing.exe . The simulator runs immediately after the download by clicking Open in the download window. Alternatively, you can first save a copy of the exe-file on any directory (folder) on your PC and then run the exe-file, which starts the simulator.

Description of the system to be simulated

Sampling of sinusoid, x(t), is simulated. The sampling results the discrete-time signal x_s(k) where k is a time index (number of samples). Both signals are plotted simultaneously. You can adjust both the signal frequency and the signal frequency.

Aim

The aim is to develop an understanding of the aliasing phenomenon.

Motivation

Sampling av continuous-time signals takes place in all applications where a computer is used to read measurement data. If the sampling rate is too low compared to the frequency of the signal to be sampled, aliasing occurs. Aliasing means that the discrete-time signal gets a lower frequency than the original signal. Obviously, sampling can cause problems in applications, e.g. in audio applications.

Theory

Given a continuous-time signal, x(t), of frequency f_cont [Hz] which is sampled with sampling frequency f_s [Hz]. The Nyquist frequency f_N is defined as half of the sampling frequency:

f_N = f_s/2

It ca be shown that if the signal frequency f_cont is larger than f_N, there is aliasing, which implies that the resulting discrete-time signal, x_s, gets a frequency, f_disc, which is smaller than the signal frequency f_cont. Figure 1 shows the relation between f_disc and f_cont.

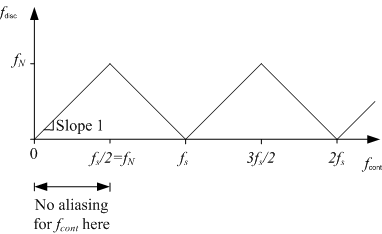
Figure 1

From the figure one observation is that f_disc is equal to the difference f_s -  f_cont if  f_cont is between f_N and f_s.

Tasks

1. Select f_cont and f_s so that there is no aliasing (cf. Figure 1). Run the simulator. Is it confirm that there is no aliasing?
   
2. Select f_cont and f_s so that there is aliasing (e.g. f_cont = 0.5 and f_s = 0.6 Hz), cf. Figure 1. Calculate from Figure 1 the resulting frequency f_disc (of the discrete-time signal). Run the simulator. Do you observe aliasing? If so, what is the frequency f_disc? Is the observation in accordance with the calculation?
   
3. What is f_disc if f_cont is equal to the Nyquist frequency? Run the simulator. Is the result confirmed?

[SimView] [TechTeach]

Updated 2 September 2017. Developed by Finn Haugen. E-mail: finn@techteach.no.