Signal Types

Snapshot of the front panel of the simulator:

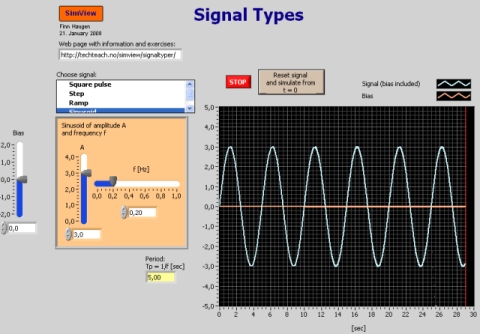
• What is needed to run the the simulator? Read to get most recent information!
• Tips for using the simulator.
• The simulator: signal_types.exe . The simulator runs immediately after the download by clicking Open in the download window. Alternatively, you can first save a copy of the exe-file on any directory (folder) on your PC and then run the exe-file, which starts the simulator.

Introduction

When you are to analyze dynamic systems (e.g. control systems, motors, thermal processes, signal filters), you may excite the system with some signal. This simulator realizes the most common test signals:

• Square pulse, which is an appoximation to an impulse
• Step, which is the most commonly used signal
• Ramp
• Sinusoid, which is used in frequency response analysis

In practice the test signal is overlayed (added to) a constant, which is denoted bias or DC component (direct current).

Tasks

1. Square pulse: Ideally an impulse is a signal of infinite amplitude and zero duration but with a finite area  men A under the signal curve. The area is also denoted the strength of the impulse. If we assume that the impulse comes at time t₀ and that it has bias B, it can be expressed as follows:

   y(t) = Ad(t - t₀) + B

   An ideal impulse can not be realized fully. An approximation is a square pulse having amplitude or height H and duration dt. The area of this signal is A = H*dt.

   Task:  Run the simulator. Select signal type "Square pulse". Observe how the signal depends on H, dt, and B, and time t₀.

    

2. Step: A step is given by

   y(t) = US(t - t₀) + B

   where U is the step amplitude or step height, and B is the bias. t₀ is the step time. S(t) is the unit step function, having amplitude 1.

   Task:  Select signal type "Step". Observe how the signal depends on U, B and t₀.

    

3. Ramp: A ramp is given by

   y(t) = KR(t - t₀) + B

   where K is the slope. B is the bias. t₀ is the starting time. R(t) is a unit ramp, having slope 1, and starting at t = 0.

   Task:  Select signal type "Ramp". Observe the signal depends on K, B and t₀.

    

4. Sinusoid: A sinusoid is given by

   y(t) = Asin(wt) = Asin(2p f t) + B

   where A is the amplitude, w is the frequency in rad/s, f is the frequency in Hertz and B is the bias. The period of the signal is

   T_p = 1/f  [sec]

   Task: Select signal type "Sinus". 

   1. Observe how the signal depends on A, f and B.
   2. Select one specific f value, and verify that the period actually is 1/f.
      

[SimView] [TechTeach]

Updated 2 September 2017. Developed by Finn Haugen. E-mail: finn@techteach.no.