Norges landbrukshøgskole, Institutt for tekniske fag

Løsning til eksamen i kurset
TML300 Reguleringsteknikk

holdt 2. desember 1999 kl. 0900 – 1400 (5 timer)

Hjelpemidler: Ingen trykte eller håndskrevne hjelpemidler. Kalkulator ikke tillatt.

Kontakt under eksamen: Finn Haugen (faglærer), tlf. 3557 5166 eller 9701 9215.

Tallene ved hver oppgave angir oppgavens relative vekt ved sensur i prosent.

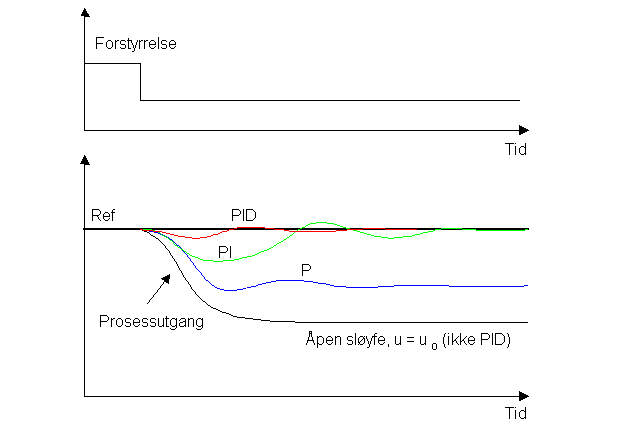
1. Se figuren nedenfor.

   

2. 1. (6) Figuren nedenfor viser et instrumenteringsskjema for temperaturreguleringssystemet basert på kaskaderegulering.

      

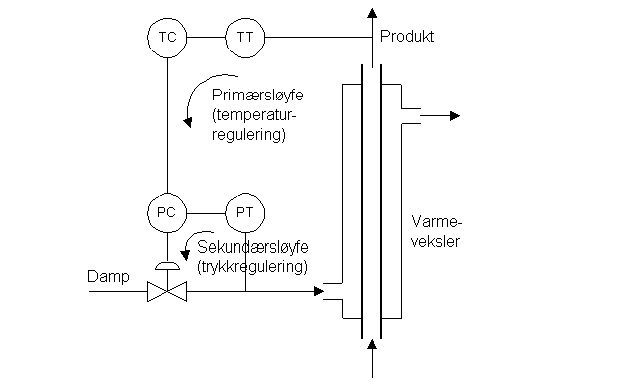
   2. (4) Fordel med kaskaderegulering: Trykkreguleringssløyfen vil kompensere for trykkvariasjoner i damptilførselen. Dette vil medføre at effekttilførselen blir jevnere, dvs. mindre påvirket av trykkvariasjonene, og dette vil igjen medføre at temperaturen får et jevnere forløp.
   
   
   
3. (5) Figuren nedenfor viser strukturen ved forholdsregulering.

   

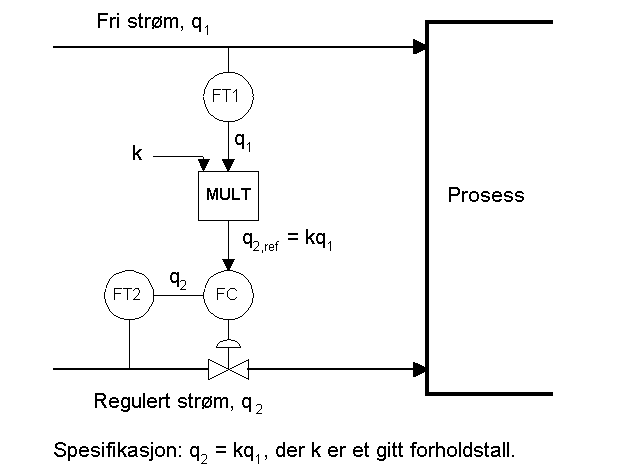
   Hensikten med forholdsregulering er å styre en massestrøm (q₂) slik at forholdet mellom denne strømningen og en annen (fri) strøm (q₁) er som spesifisert.

   
   
   
4. (7) Ideell PID-regulator:

   u(t)=u₀+u_p+u_i+u_d

   der

   u₀ er nominelt pådrag.

   u_p=K_p e er proporsjonalleddet. K_p er forsterkningen.

   u_i=(K_p/T_i) * (integralet av avviket e fra 0 til t) er integralleddet. T_i er integraltiden.

   u_d=K_pT_dde/dt er derivatleddet. T_d er derivattiden.

   
   
   
5. (8) Finn amplitudefunksjonen og fasefunksjonen for frekvensresponsen for transferfunksjonen

   h(s)=K(T1*s+1)*e^-Ts/(T2*s+1)

   Frekvensresponsen er

   h(jw)=K(T₁jw+1)*e^-Tjw/(T₂w+1)

   Ved å skrive telleren på polarform og nevneren på polarform, fås

   Amplitudefunksjonen=|h(jw)|=K×sqrt(T₁²w²+1)/sqrt(T₂²w²+1)

   Fasefunksjonen=arg[h(jw)]=arctan(T₁w) - arctan(T₂w) - Tw[rad]

6. (4) Den tilsvarende statiske responsen i y blir

   y_s=h(s)|_s=0×U=KU

7. 1. (6) Skriver modellen på formen

      dx/dt=(1/a)(bx+cu)
      y=dx + eu

      Blokkdiagrammet er vist i figuren nedenfor.

      

   2. (6) Laplacetransformasjon av modellen gir

      asx(s)=bx(s)+cu(s)
      y(s)=dx(s) + eu(s)

      Eliminering av x(s) mellom ovenstående to likninger og ordning av det resultarende uttrykket gir følgende transferfunksjon fra u til y:

      y(s)/u(s)=dc/(as+b) + e

   
   
   
8. 1. (2) lsim simulerer en lineær, tidsinvariant modell (transferfunksjon eller tilstandsrommodell) for brukergenererte inngangsvariable (av vilkårlig type).
   2. (2) tf definerer et LTI-objekt av typen transferfunksjon.
   3. (2) bode plotter (i et Bodediagram) og/eller beregner frekvensresponsen for et LTI-objekt.
9. (9) Modellen baseres på massebalanse:

   dm/dt=rq₁ - rq₂

   som med m=Arh og q₁=Ku innsatt og deretter med r forkortet, gir

   Adh/dt=Ku- q₂

10. (4) Transferfunksjonen for et system som har forsterkning 3 og tidskonstant 7 [sek]:

    h(s)=K/(Ts+1) der K=3 og T=7

11. (6)
    • Reguleringssløyfen koples opp.
    • Regulatoren skal være en P-regulator, hvilket oppnås med T_i så stor som mulig og T_d=0.
    • K_p settes lik null.
    • Det nominelle pådrag u₀ justeres slik at prosessen holdes i arbeidspunktet (dvs. slik at prosessutgangen er lik referansen eller settpunktet).
    • K_p økes inntil det oppstår stående svingninger i sløyfen. Den tilsvarende K_p beregnes den kritiske K_p=K_pk. Periodetiden T_k i svingningene (kan observeres f.eks. i pådraget eller prosessmålingen) måles.
    • PID-parametrene beregnes som funksjoner av K_pk og T_k ihht. Z-N-formlene.
    • De beregnede regulatorparametrene legges inn i regulatoren.
    
    
    
12. (6) Fordi prosessdynamikken varierer med massestrømmen, og når prosessdynamikken varierer, bør (må, i visse tilfeller) regulatorparametrene justeres slik at regulatioren til enhver tid er tilpasset prosessdynamikken, slik at reguleringssystemet har tilfredsstillende stabilitet og raskhet. Mer presist: Jo mindre massestrømmen er, jo større vil forsterkningen og tidsforsinkelsen (og tidskonstanten) være, og dersom regulatorparametrene ikke justeres i overensstemmelse med disse endringene, vil reguleringssystemet få dårligere stabilitet.
    
    
13. (6) En generell 2. ordens lineær tilstandsrommodell med 1 inngangsvariabel og 2 utgangsvariable (modellen dekker alle konkrete eksempler på slike modeller):

    dx₁/dt=a₁₁x₁+a₁₁x₁ + b₁u
    dx₂/dt=a₂₁x₁+a₂₂x₂+b₂u
    y₁=c₁₁x₁+c₁₂x₂+d₁u
    y₂=c₂₁x₁+c₂₂x₂+d₂u

    eller

    dx/dt=Ax+Bu
    y=Cx+Du

    der (i Matlab-notasjon)

    x=[x₁; x₂]
    u=u (skalar)
    y=[y₁; y₂]

    A=[a₁₁, a₁₂; a₂₁a₂₂]
    B=[b₁; b₂]
    C=[c₁₁, c₁₂; c₂₁c₂₂]
    D=[d₁; d₂]

[Kursets hjemmeside]

Oppdatert 8.12.99 av Finn Haugen (e-post: Finn.Haugen@hit.no).