DC-Motor

Snapshot of the front panel of the simulator:

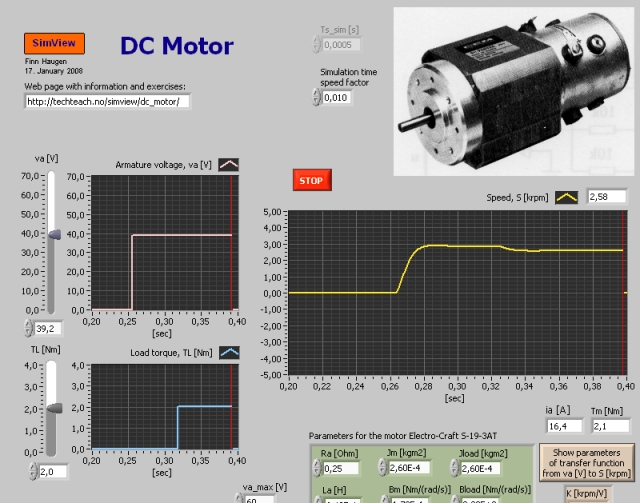
• What is needed to run the the simulator? Read to get most recent information!
• Tips for using the simulator.
• The simulator: dc_motor.exe . The simulator runs immediately after the download by clicking Open in the download window. Alternatively, you can first save a copy of the exe-file on any directory (folder) on your PC and then run the exe-file, which starts the simulator.

Introduction

DC-motors are used in many servo mechanisms. Compared to other electric motors, DC-motors are easy to model mathematically.

The DC-motor simulated is the Electro-Craft S-19-3AT which is an armature controlled DC-motor. The motor parameters are given on the front panel of the simulator.

Theory

In the expressions below the following quantities are used: S is rotational speed. v_a is armature voltage. i_a is armature current. T_f  is friction torque. T_L is load torque. J is the sum of the intertias of the motor and the load, i.e. J = J_motor + J_load. B is the sum of the damping coefficients of motor and load. L_a is the armature inductance. R_a is the armature resistance. K_e is the voltage constant (the so called back-emf constant). K_T is the torque constant.

Dynamic model (differential equation)

A mathematical model of the motor can be found from the Kirchhoff's voltage law on the armature circuit and the torque balance of the mechanical rotation:

Kirchhoffs voltage law yields

(1) L_adi_a/dt = v_a - R_ai_a - K_eS

Torque balance yields

(2) JdS/dt = K_Ti_a - BS - T_f - T_L

Transfer function model

By taking the Laplace transform of the model above we will find the following transfer function from armature voltage v_a to speed S:

(3) S(s)/v_a(s) = H(s) = K/[(s/w₀) + 2z(s/w₀) + 1]

where the parameters are as follows:

Gain:

(4) K = K_t/(K_tK_e+BR_a) [rpm/V]

Relative damping factor:

(5) z = 0.5*(JR_a+BL_a)/[sqrt(JL_a(K_tK_e+BR_a))]

Undamped resonance frequency:

(6) w₀ = sqrt[(K_tK_e+BR_a)/(JL_a)] [rad/s]

Static model

By setting the derivatives in (1) and (2) equal to zero and eliminating i_a, we get the following static model (all variables are assumed to have constant values):

(7) S = [K_t/(K_tK_e+BR_a)]v_a - [R_a/(K_tK_e+BR_a)](T_f + T_L)

Tasks

1. Assume that the armature voltage v_a is 30 volt and that the motor parameters have values equal to the default values (can be recalled using the menu Operate / Reinitialize All to Default on the front panel of the simulator).
   1. Find the static speed (using simulation).
   2. Calculate the static speed from the static model (7). Is the answer in accordance with the result found in task 1a?
2. See equation (5). How are the relative damping factor and the undamped resonance frequency changed if the total inertia J increases? Is the result confirmed in a simulation (qualitatively)?
3. Confirm both from the model and from simulations that the statis speed is independent of the inertia.
4. Use the default values of the motor parameters.
   1. What is the value of w₀ (you can read it off from the simulator front panel)?
   2. In general the response time (the 63% raise time of the step response) of a second order system is approximately equal to 1.5/w₀ [sec]. Calculate from this the response time of the motor. Is the result in accordance with a simulated step response?

[SimView] [TechTeach]

Updated 2 September 2017. Developed by Finn Haugen. E-mail: finn@techteach.no.