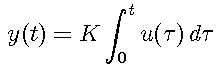Integrator

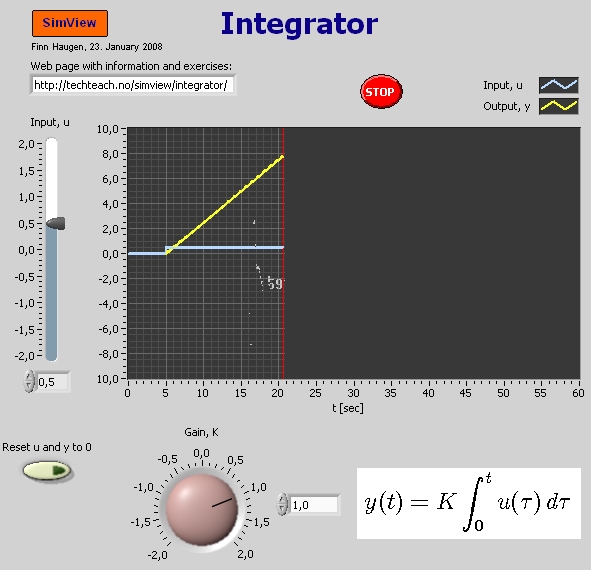
Snapshot of the front panel of the simulator:

• What is needed to run the the simulator? Read to get most recent information!
• Tips for using the simulator.
• The simulator: integrator.exe . The simulator runs immediately after the download by clicking Open in the download window. Alternatively, you can first save a copy of the exe-file on any directory (folder) on your PC and then run the exe-file, which starts the simulator.

Description of the simulated system

In this simulator a general integrator is simulated. You can freely adjust the input signal u(t) and the gain of the integrator, K.

The relation between the input signal u and the output signal y can be expressed with the following integral equation:

This integral equation is equivalent with the following differential equation:

dy(t)/dt = Ku(t)

The transfer function of the integrator is

h(s) = y(s)/u(s) = K/s

The simulator is based on discretizing the integrator with the Runge-Kutta second-order method with time-step of 0.05 sec.

Aims

The aims of the simulator is to give insight into the dynamic behaviour of an integrator.

Motivation

There are many dynamic systems with interating behaviour, e.g.:

• Liquid tanks where the outflow is level is independent of the level, as if the outflow is produced by a pump. In such a system the pump control signal can be the input variable and the level is the output variable of the integrator.
• Thermal systems without heat loss to the environment. The iInput variable is heat supply (via a heatring element), and the output variable is the temperature.
• A motor having neglectable (or very quick) dynamics. The input variable is the motor control signal, and the output variable is the motor rotational position.
• The integrator-term of a PID-controller. The input variable is the control error, and the output variable is the integrator term, u_i.

Tasks

Below, U is the amplitude of the input step, and K is the gain of the integrator.

1. The shape of the step response: Set K = 1. Simulate with an input step amplitude of U = 1. Characterize the shape of the step response.

   
   

2. The importance of the gain K: Simulate with input step amplitude U = 1 for different values of K, both positive and negative. How does the slope of the step response depend on K?

   
   

3. The integrator effect: Simulate while adjusting the input u(t). Do you see that the integrator actually integrates ("stores") the input?

    

[SimView] [TechTeach]

Updated 23. January 2008. Developed by Finn Haugen. E-mail: finn@techteach.no.