RC-Circuit

Snapshot of the front panel of the simulator:

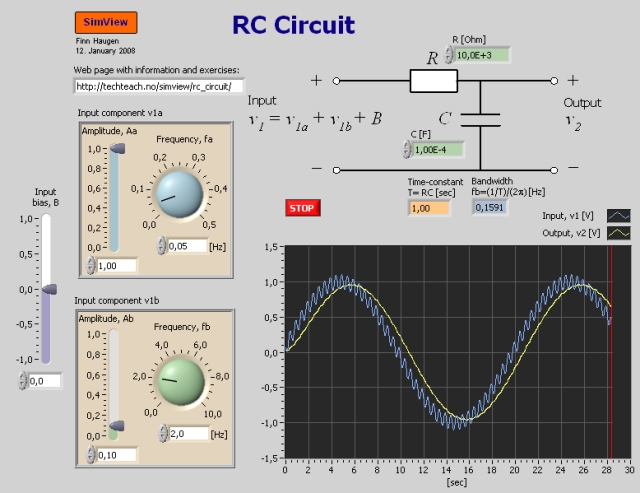
• What is needed to run the the simulator? Read to get most recent information!
• Tips for using the simulator.
• The simulator: rc_circuit.exe . The simulator runs immediately after the download by clicking Open in the download window. Alternatively, you can first save a copy of the exe-file on any directory (folder) on your PC and then run the exe-file, which starts the simulator.

Description of the simulated system

In this simulator an RC-circuit is simulated. It consists of a resistor R [Ohm] and a capacitor C [Farad] connected in a circuit, see the front panel of the simulator.

In the tasks below the dynamic properties of the RC-circuit will be observed through simulations. In the simulator the input signal is a sum of two independent sinusoids and a bias (a constant).

Aim

The aim of this simulator is to increase the understanding of the RC-circuit as a dynamic system.

Motivation

In applikations where a simple analog lowpass filter is needed, the RC-circuit is commonly used, as in I/O equipment (input/output) for attenuation of measurement noise.

Mathematical model

It can be shown that the relation between the input voltage v₁ and the output voltage v₂ is given by the following differential equation:

(1) RC*dv₂/dt = v₁ - v₂

By taking the Laplace transform of this differencial equation we find the following transfer function, H(s), from v₁ to v₂:

(2) H(s) = 1/(Ts+1)

where

(3) T = RC [s]

is the filter time constant.

Using frequency response theory, it can be found that the bandwidth of the filter is

(4) f_b = (1/T)/(2p) [Hz]

Tasks

Unless otherwise stated you should use default values of the various parameters (you get the the default value via right-click on the front panel element).

1. The step resonse of the filter: In this subtask, you should suppress the sinusoids (by setting the amplitudes to zero).
   1. Calculate (by hand) the time constant T according to Eq. (3) above. Is the result the same as can be seen on the front panel of the simulator when the simulator runs? Then run a simulation where you adjust the signal component B as a step, and read off the time constant from the response. Is the observed time constant the same as the calculated time constant?
   2. Run a simulation with some constant input signal, say V₁. What is the corresponding steady-state value, v_2s, of the output voltage response? From these results, what is the relation between V₁ and v_2s? Can you calculate this relation directly from the model (1)?

   
   

2. Frequency response of the filter: Set the signal component B to zero. Use default values of R and C.
   1. Let the sinusoid v_1a have amplitude 0.5 and frequency 0.05Hz, and let sinusoid v_1b have amplitude 0.5 and frequency 1Hz. Thus, signal component v_1a has a smaller frequency than the bandwidth, which is 0.16Hz, while the component v_1b has larger frequency than the bandwidth. In other words, v_1a are in the passband of the filter, while v_1b is in the stoppband of the filter. Run the simulator! Can you observe from the simulation that signal component  that component 1 is in the passband, while v_1b is in the stoppband?
   2. The bandwidth is defined as the frequency where the amplitude gain of the filter is 1/sqrt(2) =  0.71 = -3dB. In other words, if the sinusoidal input signal has frequency equal to the bandwidth, the amplitude of the output signal is 71% of the amplitude of the input signal. Verify this by running a simulation.

    

[SimView] [TechTeach]

Updated 27 August 2017. Developed by Finn Haugen. E-mail: finn@techteach.no.