Poles and Stability of Feedback System

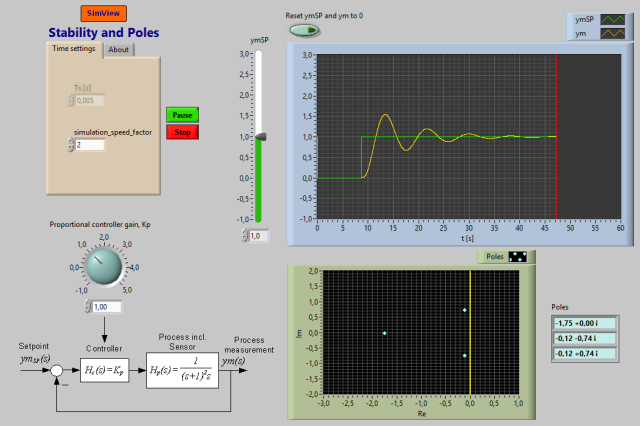
Snapshot of the front panel of the simulator:

• What is needed to run the the simulator? Read to get most recent information!
• Tips for using the simulator.
• The simulator: stability_poles.zip (unzip, and open stability_poles.exe).

Description of the simulated system

In this simulator a feedback system, namely a control system, is simulated. The controller is a P controller. The front panel of the simulator shows a block diagram of the control system.

It can be shown that the transfer funcion from setpoint ymSP to process measurement ym is

ym(s)/ymSP(s) = [H_c(s)H_p(s)]/[1 + H_c(s)H_p(s)]

= K_p/(s³+2s² + s + K_p)

= K_p/a(s)

where a(s) is the characteristic polynomial.

The stability property of the feedback system can be determined from the poles, which are the roots of the characteristic equation:

a(s) = s³+2s² + s + K_p = 0

In the simulator the controller gain K_p can be adjusted in real time, and the response in the process measurement and the poles are shown.

Aims

The aim of this simulator is to observe the connection between stability and pole placement.

Tasks

1. The poles of the control system depend on the controller gain K_p, which can be adjusted. The poles are displayed on the front panel of the simulator. Find, by looking at the poles, for which range of values of K_p (both negative and positive values of K_p should be checked) the feedback system is:
   • asymptotically stable
   • marginally stable
   • unstable
2. Select one K_p value for each of the three cases described above. For each such K_p: Does the step response confirm the stability property as determined by pole placement? (Apply a step at the setpoint.)

[SimView] [TechTeach]

Updated 18 October 2017. Developed by Finn Haugen. E-mail: finn@techteach.no.