Correlation

Snapshot of the front panel of the simulator:

• What is needed to run the the simulator? Read to get most recent information!
• Tips for using the simulator.
• The simulator: correlation.exe . The simulator runs immediately after the download by clicking Open in the download window. Alternatively, you can first save a copy of the exe-file on any directory (folder) on your PC and then run the exe-file, which starts the simulator.

Description of the system to be simulated

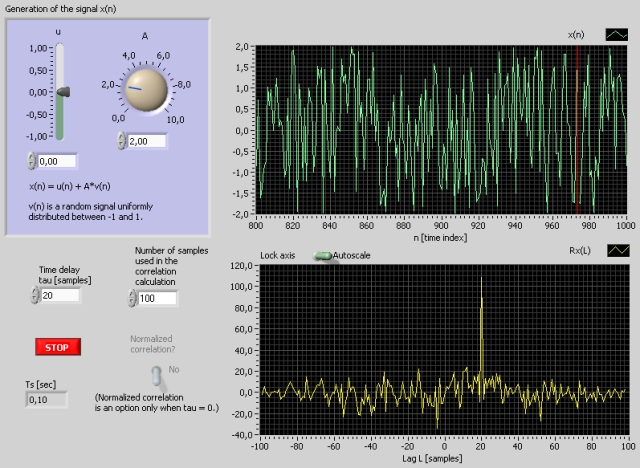
The user can generate a signal x(n) as sum of a constant (or bias) and a random signal. The auto correlation of x(n) is calculated in real time based on a number of samples (of historical data) defined by the user.

The user can also introduce a lag L [samples] between signals. The cross correlation of the signal and the delayed signal is computed.

Aims

The aims of this simulator is as follows:

• How the correlation function works
• How the correlation function represents random signals
• How the cross correlation function represents a time delay between random signals

Motivation

The autocorrelation of a signal can be used to express the random character of a signal.

The cross correlation can be used to detect a time delay between two signals.

Tasks

Initially, choose

• non-normalized correlation
• zero lag between the signals (time series)

1. Auto correlation of a constant signal: Let x(n) be a constant.
   1. Use a non-normalized correlation function. What is the value of the correlation R_x(0)? Could you have calculated R_x(0) in advance?
   2. Can you from the shown R_x(L) in the simulator determine which kind of correlation the correlation function implemented in LabVIEW implements? (Is there avaraging, i.e. division by number of samples N? Is there a compensation in the correlation function for large L-values?)

    

2. Auto correlation of a random signal: Let x(n) be a pure random signal with zero mean.
   1. Does the form of the correlation function R_x(L) indicate that the signal is ransom (with zero bias)?
   2. Use a normalized correlation function R_x. Describe the difference between this R_x and the non-normalized correlation?
   3. Does R_x clearly express the dandomness of a signal if the number of samples of the signal of which the correlation function is calculated, is small?
   4. Select non-normalized correlation. Read off the energy of x from the correlation function.

    

3. Correlation of lagged random signals: Let x(n) be a random signal with zero mean. Introduce some lag in the signal. Use non-normalized correlation. The correlation is now being calculated between x(n) and x(n-L).
   1. In which way is the lag expressed by the correlation function? (You may try with different lags.)

[SimView] [TechTeach]

Updated 2 September 2017. Developed by Finn Haugen. E-mail: finn@techteach.no.