Kalman Filter
Snapshot of the front panel of the simulator:
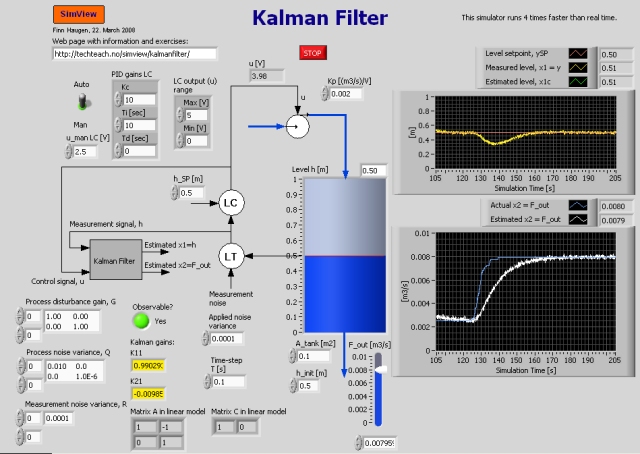
- What is needed to run the the simulator? Read to get most recent information!
- Tips for using the simulator.
- The simulator: kalmanfilter.zip (unzip, and open kalmanfilter.exe).
Aims
The aim of this simulator is to show how a Kalman Filter can be used to continuously estimate the value of an unknown process variable. The typical trade-off is demonstrated: You can not have both fast estimate update and noise-attenuated estimates, i.e. you have to choose to emphasize either of them.
Motivation
The Kalman Filter is a generic algorithm for estimating process variables, assuming that you have a mathematical model of the process (a set of differential equations) and that there is at least one variable that is continuously measured. The Kalman Filter is used in a large variety of applications - in control applications where the controller uses estimates as if they were real measurements and in supervisory systems (as "soft-sensors").
Description of the simulated system
The process is a water tank with inflow and outflow. The level is maintained at or close to a level setpoint by a level controller which controls the inflow. The outflow, which is regarded as a disturbance to the process, can be adjusted freely by the user. A Kalman Filter is used to estimate the assumed unknown outflow. Detailes about the model and the Kalman Filter are described in kalmanfilter.pdf.
Tasks
1. Change the outflow Fout arbitrarily, but keep it constant for a while, too. Is the Kalman Filter able to estimate Fout correctly in steady-state?2. In an attempt to make the estimate converge faster to the real value, the assumed process disturbance variance Q22 of state x2 (which is the outflow) can be increased. What is the impact on the state-estimate (benefit and drawback)? Simultaneously, observe how the Kalman Gain K21 is changed accordingly. Does this change of K21 make sense?
3. Also the assumed measurement variance R influences the state-estimates. Descrease R. What is the impact on the state-estimate (benefit and drawback)? Simultaneously, observe how the Kalman Gains K21 are changed accordingly. Does these changes of make sense?
Updated 2 September 2017. Developed by Finn Haugen. E-mail: finn@techteach.no.
