Mass-Spring-Damper

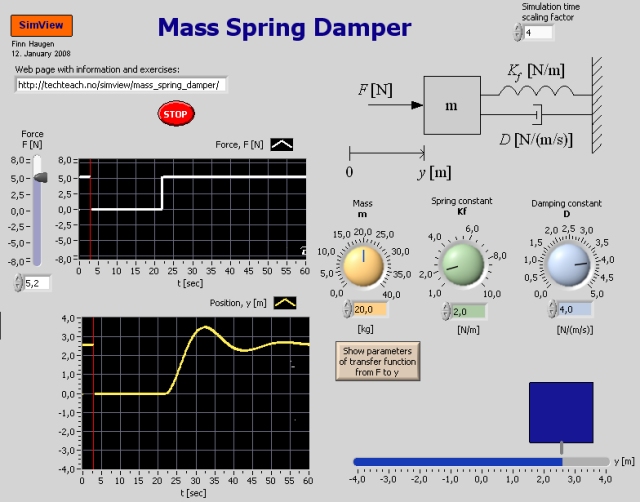
Snapshot from the front panel of the simulator:

• What is needed to run the the simulator? Read to get most recent information!
• Tips for using the simulator.
• The simulator: mass_spring_damper.exe . The simulator runs immediately after the download by clicking Open in the download window. Alternatively, you can first save a copy of the exe-file on any directory (folder) on your PC and then run the exe-file, which starts the simulator.

Description of the simulated system

A mass-spring-damper system is simulated, see the front panel of the simulator. You can adjust the force acting in the mass, and the position response is plotted.

The mathematical model of the system can be derived from a force balance (or Newton's second law: mass times acceleration is equal to the sum of forces) to give the following second order differential equation:

mdx²/dt² = -Ddx/dt - K_f x + F

where

• x [m] is the position of the mass
• F [N] is the force acting on the mass
• m [kg] is the mass
• D [N/(m/s)] is the damping constant (Ddx/dt is the damping force)
• K_f [N/m] is the spring constant (K_fx is the spring force)

It can be shown that the transfer function from force F to position x is a second order tramsfer function with the following standard parameters:

K = 1/K_f

z = D/[2*sqrt(mK_f)]

w₀ = sqrt(K_f/m)

The values of the above parameters can be seen on the front panel of the simulator.

Aim

The aim of the simulator is to develop an understanding of the dynamic properties of a mass-spring-damper.

This simulator can develop a "physical" interpretation of the standard parameters of second order systems. (This assumes you master the theory of of second order systems.) However, you may benefit well from working with most of the tasks below even if you do not master this theory (you can skip tasks 1d, 2d and 3d).

Motivation

The mass-spring-damper system is a standard example of a second order system, since it relatively easy to give a physical interpretation of the model parameters of the second order system.

Tasks

Unless otherwise stated, it is assumed that you use the default values of the parameters.

1. The importance of mass m:  
   1. How does the mass m influence the speed of the transient response (the transient response is the first part of the response - before it stabilizes)?
   2. How does the mass m influence the damping of the transient response? (There is small damping if the response oscillates much.)
   3. How does the mass m influence the stationary response (which is the response as time goes to infinity)?
   4. Observe at the front panel how the standard parameters of the second order systems (K, z, w₀) depend on m. Are the observations in accordance with the above expressions of these parameters?

   
   

2. The importance of the spring constant K_f: 
   1. How does the spring constant K_f influence the speed of the transient response (the transient response is the first part of the response - before it stabilizes)?
   2. How does the spring constant K_f influence the damping of the transient response? (There is small damping if the response oscillates much.)
   3. How does the spring constant K_f influence the stationary response (which is the response as time goes to infinity)?
   4. Observe on the front panel how the standard parameters of the second order systems (K, z, w₀) depend on K_f. Are the observations in accordance with the above expressions of these parameters?

   
   

3. The importance of the the damping constant D:
   1. How does the damping constant D influence the speed of the transient response (the transient response is the first part of the response - before it stabilizes)?
   2. How does the damping constant D influence the damping of the transient response? (There is small damping if the response oscillates much.)
   3. How does the damping constant D influence the stationary response (which is the response as time goes to infinity)?
   4. Observe on the front panel how the standard parameters of the second order systems (K, z, w₀) depend on D. Are the observations in accordance with the above expressions of these parameters?

   
   

4. The importance of the constant force F_s:  Observe the step response in x for various F_s. How does the stationary value of the step response, x_s, depend on F_s?
   

[SimView] [TechTeach]

Updated 3. June 2009. Developed by Finn Haugen. E-mail: finn@techteach.no.