Multivariable Control Using Linear Decoupling

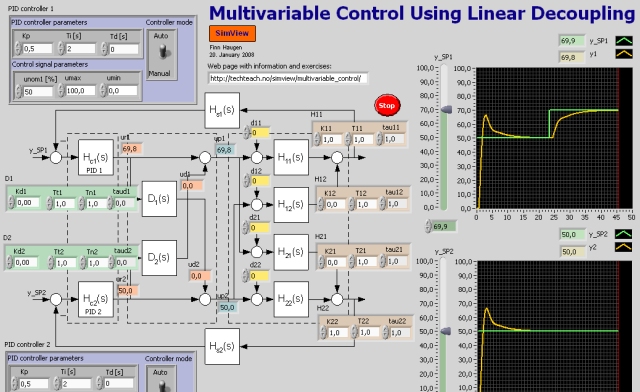
Snapshot of the front panel of the simulator:

• What is needed to run the the simulator? Read to get most recent information!
• Tips for using the simulator.
• The simulator: multivariable_control.exe . The simulator runs immediately after the download by clicking Open in the download window. Alternatively, you can first save a copy of the exe-file on any directory (folder) on your PC and then run the exe-file, which starts the simulator.

Description of the system to be simulated

I this simulator a 2x2 multivariable system represented by a model consisting of 4 transfer functions - one in each of the 4 couplings between the 2 control variables and the 2 output variables. Each of the transfer functions is a "first order with time delay":

y_i(s)/u_j(s) = H_ij(s) = K_ij(e^-t_ijs)/[(T_ijs + 1)]

Aim

The aims of this simulator is to give an understanding of the dynamics of a multivariable process, to give experience with controller tuning, and to observe the benefits of using decoupling.

Motivation

Multivariable processes may be difficult to control due to cross couplings in the process, which causes interaction between the control loops. The PID controller tuning shoould follow certain procedures. Using a decoupler between the PID controllers and the process may give better control. Linear decouplers are available in some commercial control systems.

Tasks

1. Configuring a process without cross couplings:
   1. Choose parameter values of the process transfer functions (but you may keep the default values), but it is required in this subtask that the process has no cross couplings.
   2. Verify the process dynamics (as expresses by the transfer functions) by running some setp response tests (steps in the control variables with the controllers in manual mode). In particular, verify that there are no cross couplings in the process.

       

2. Controlling a process which does not have cross couplings:
   1. Tune the PID controllers.
   2. Show (using simulations) that there the control loops does not interact.

    

3. Single loop control of a process which has cross couplings:
   1. Choose process parameters so that the process has cross couplings (in both directions), e.g. K12 = K21 = 0.5, and time delays equal to 0.5, and time constants equal to 1. Verify (using simulations) that there are cross couplings in the process.
   2. Keep the the PID settings from task 1.
      1. Verify (using simulations) that there are interactions between the control loops.
      2. What happens to the stability of the control system if the cross couplings becomes stronger (you can increase the proper gains)? Adjust the PID parameters so that the stability again is acceptable.
      3. Tune the PID controller using the following procedure:

         (1) Tune the controller in each of the loops in turn with all the other controllers in manual mode. (2): Close all the loops (set all controllers in automatic mode). (3) If there are stability problems, reduce the gain and/or increase the integral time of the controllers in the least important loops.

    

4. Control based on decoupling:

   Keep the process parameter values from Task 3 above.

   1. Find a decoupler for the process (calculate the parameters of the transfer functions in the decoupler from the process model). Show (using simulations) that the decoupling works (run step response tests of the process, with the controllers in manual mode).
   2. Tune the PID controllers for the process including the decoupler. Show (using simulations) that there is no interaction between the control loops. (Note: You may observe a steady state control error even though there is integral action on the controllers. This may stem from saturation in the control signal as it tries to compensate for the disturbance which the cross couplings represents.)

[SimView] [TechTeach]

Updated 2 September 2017. Developed by Finn Haugen. E-mail: finn@techteach.no.