White and Coloured Noise

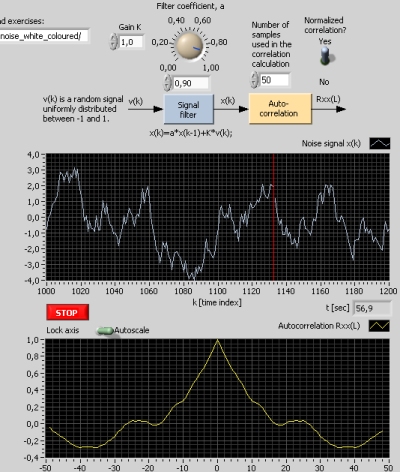
Snapshot of the front panel of the simulator:

• What is needed to run the the simulator? Read to get most recent information!
• Tips for using the simulator.
• The simulator: noise_white_coloured.exe . The simulator runs immediately after the download by clicking Open in the download window. Alternatively, you can first save a copy of the exe-file on any directory (folder) on your PC and then run the exe-file, which starts the simulator.

Description of the simulated system

A noise signal, v(k), being a uniformly distributed random signal is generated. Thus, v is white noise, which means it varies principally completely randomly between the samples. This signal is sent to the following discrete-time signal filter - also denoted shaping filter:

x(k) = a*x(k-1) + K*v(k)

where a is a filter parameter and K is a gain. With a = 0, the filter output signal, x, is also white noise. With parameter between 0 and 1, x becomes coloured noise, which means it does not vary completely randomly between the samples. The autocorrelation of x, R_xx(L), is plotted. L is the lag parameter. R_xx(L) shows the "colour" of x.

Aims

• To see typical plots of white noise and coloured noise.
• To observe how the autocorrelation function expresses the "colourness" of a signal.

Motivation

White noise and coloured noise are important signals in stochastic systems. For example, in applications as minimum variance optimal control and in state estimation using a Kalman filter the noise signals acting on the system (for control or estimation) are assumed to be white. If the noise is coloured, it can be regarded as the output of a dynamic signal filter typically called a shaping filter.

Tasks

1. White noise: Set parameter a = 0, causing x to be white noise. Also set the gain K = 1.
   1. Observe the signal x. Can you clearly see the random characteristics of the signal?
   2. Observe the autocorrelation R_xx(L). For ideal white noise the normalized R_xx(L) is 1 for lag L = 0, and 0 for other values of L. Why does the autocorrelation of x differ from the ideal form of R_xx(L).
2. Coloured noise:
   1. Initially, set a = 0. Also set the gain K = 1.
   2. Increase the parameter a continuously. Observe how the shape of the signal x changes. Does it become less random? Explain thsi from the shaping filter model. Simultaneously, observe the autocorrelation R_xx(L). How does its shape change as parameter a increases? Explain!

[SimView] [TechTeach]

Updated 19. January 2008. Developed by Finn Haugen. E-mail: finn@techteach.no.