Transfer Function Based PID Tuning
Snapshot of parts of the front panel of the simulator:

- What is needed to run the the simulator? Read to get most recent information!
- Tips for using the simulator.
- The simulator: pidtuning.exe . The simulator runs immediately after the download by clicking Open in the download window. Alternatively, you can first save a copy of the exe-file on any directory (folder) on your PC and then run the exe-file, which starts the simulator.
Description of the simulated system
Introduction
The control system of a process given by a transfer function model is simulated. You can adjust the setpoint and the disturbance. To quantize the performance of the controller the IAE performance index (Integral of Absolute value of control Error) is calculated continuously:
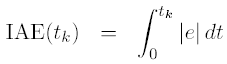
We can say that the less IAE index, the better control. (However, the IAE index does not express the control usage, so it may happen that the control usage is abrupt, causing wear on mechanical actuatorsas valves, motors and pumps.)
In the tasks below the controller shall be tuned based on the transfer function model of the process to be controlled. Several methods are available, e.g. The Ziegler-Nichol's methods; Pole-zero cancellation, and the Skogestad's method [S. Skogestad: Simple Analytical Rules for Model Reduction and PID Controller Tuning, J. Process Control, 2002], see also Ch. 8 in PID Control.
The controlled process
The process model which is controlled in this simulator can be chosen you. By default the transfer function from control variable, u, to measurement signal, y, is a second order transfer function with time-delay, with a disturbance, v, acting on the process at the same place dynamically as the control variable. That is, the process model is on the following form:
y(s) = Hps(s)u(s) + Hps(s)v(s)
where you can select Hps(s) quite freely (any numerator and denumerator polynomials, with or without time delay).
The nominal operating point
The nominal operating point is characterized as follows:
- The process measurement ym is 50 (in a proper unit)
- The disturbance is 10.
- The nominal control signal, u0, which keeps the process in or close to the operating point, is 40.
Controller function
The PID controller is on serial form, i.e. its transfer function is
Hc(s) = Kp [(1+Tis)(1+Tds)]/[Tis(Tfs+1)]
Aim
The aim of this simulator is to give practice in tuning a PID controller for a process given by its transfer function model.
Motivation
If a transfer function model of the process to be controlled is known (with good accuracy), a controller can be tuned from the transfer function directly, i.e. the controller parameters are calculated as functions of the transfer function model. Such model based tuning is beneficial compared to experimental tuning since no experiment is required. However at least simulations should be run to check if the tuning is acceptable (assuming the process model is accurate).
Tasks
In the tasks below it is assumed that the process initially is in the nominal operating point.
- Ensure that the process model is a second order transfer function, Hp(s), consisting of a series connection of two time constant subsystems having time constants 1s and 0.5s respectively, and a time delay 0.3s. The gain of the combined transfer function is 1.
- Tune a PID controller for the above process using the different
methods given below. Compare the tuning methods by comparing the IAE index after a disturbance step.
The tuning methods you can use are
- Ziegler-Nichols' closed loop method
- Skogestad's method with k1 = 4, cf. Table 8.2 in PID Control
- Skogestad's method with k1 = 1.44, cf. Table 8.2 in PID Control
Updated 17. April 2008. Developed by Finn Haugen. E-mail: finn@techteach.no.
