LQ Optimal Control of Inverted Pendulum

Snapshot of the front panel of the simulator:

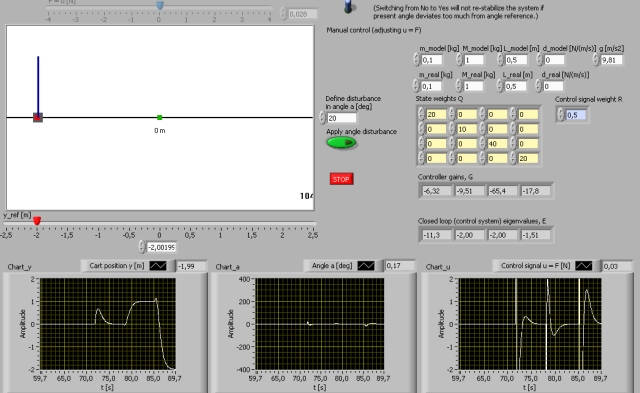
• What is needed to run the the simulator? Read to get most recent information!
• Tips for using the simulator.
• The simulator:pendulum.zip (unzip, and open pendulum.exe).

Description of the simulated system

pendulum_model.pdf gives a mathematical desciption of the system - the cart with pendulum, and the stabilizing control system.

Aims

Aims of this simulator is to see how LQ control quite easily can be used to solve a difficult control problem, namely stabilizing an unstable process.

Motivation

The LQ controller is a very powerful control law because it always stabilizes a process, and because the tuning of the controller is quite intuitive via the weights of the states and the control variables in the optimization criterion.

Although the pendulum itself is not a particularly useful process, it has many similarities to important processes:

• In upright position - it is then called an inverted pendulum - it is similar to a rocket being launched.
• In downright position - it is then an ordinary pendulum - it is similar to a crane with load.

Tasks

Unless otherwise stated, set the parameters back to default values after each of the tasks. (This can be done via Edit / Reintialize values to default.)

1. Select upright stabilization.
   1. Is the controller able to stabilize the pendulum after an angle disturbance at any cart position reference (try a number of different references)?
   2. Theoretical question: How can you change one of the elements of the Q matrix to obtain more damped movement of the cart? Is this verified in a simulation?
   3. Theoretical question: How can you change the (one) element of the R matrix to obtain smoother control action?Is this verified in a simulation? Is it also verified in the eigenvalues of the control system?
   4. What is the maximum angle disturbance that the control system can handle?
   5. To check the robustness of the control system: Assume that the real cart mass, M_real, is different from the mass, M_model, assumed in the design of the controller. Assume that M_model = 1 kg. What is the minimum M_real and what is the maximum M_real that the control system can handle (before it becomes unstable)? (Find the answer using simulations.)
2. Select downright stabilization.
   1. Set the controller in manual control mode. Apply a disturbance to the pendulum angle. Try to stabilize the pendulum at zero cart position. Easy or difficult?
   2. Set the controller in automatic control mode. Is the controller able to stabilize the pendulum after an angle disturbance at any cart position reference (try a number of different references)? Is the automatic feedback control better than the manual control?
   3. Observe that the controller parameters in the downright operating point and in the upright operating point are different. Why are they different?

[SimView] [TechTeach]

Updated 8. February 2008. Developed by Finn Haugen. E-mail: finn@techteach.no.