Lowpass Filter
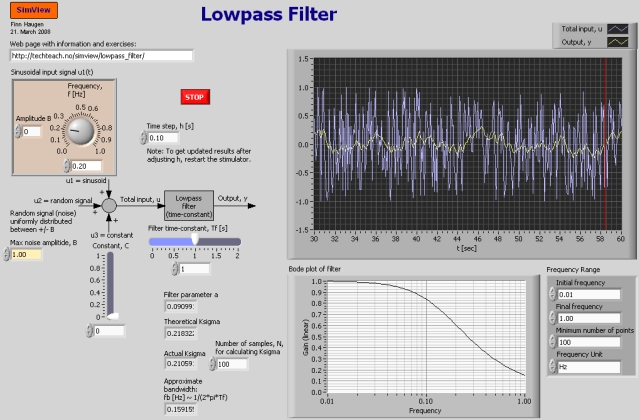
Snapshot of the front panel of the simulator:
- What is needed to run the the simulator? Read to get most recent information!
- Tips for using the simulator.
- The simulator: lowpass_filter.zip (unzip, and open lowpass_filter.exe)
Aims
The aims of this simulator are:
- Demonstrate how a time-constant filter attenuates sinusoidal signals (noise)
- Demonstrate how a time-constant filter attenuates random signal (random noise)
Motivation
Lowpass filters are frequently needed in practical application based in some processing of measurements. This is because all practical measurements are noisy. Typically the noise is approximately a random signal. The filter is used to attenuate the noise.
One very important application is in a control system. The process measurement (temperature, level, pressure, speed etc.) always contains some noise. If the noise is not attenuated it will propagate through the controller and cause abrupt (noisy) variations in the control signal, causing excessive wear of the actuator (pump, valve, motor).
The filter algorithm given above is relatively simple, but still it is probably the most commonly used filter algorithm in practical application.
Description of the system that is simulated
Input signals to the filter
A discrete-time first order filter is simulated. The input signal to the filter consists of three additive terms:
- A sinusoidal signal
- A random signal (white noise)
- A constant (or bias)
Each of these signals can be deactivated (removed). The (total) input and the output signals are plotted in real time in a chart. Also, the amplitude gain plot (Bode plot) of the filter is plotted.
The filter function
The filter is a discretized version of a continuous-time time-constant filter given by the following s-transfer function:
H(s) = Y(s)/U(s) = 1/(Tfs+1)
The user can select the following filter parameters:
- The filter time-constant, Tf [s]
- The filter (and the simulator) time-step, h [s]
The filter algorithm that is implemented in the simulator is given by the following difference equation:
y(tk) = (1-a)*y(tk-1) + a*u(tk) (Eq. 1)
where tk is the discrete point of time at time index k. Hence, tk-1 means the previous discrete point of time. y is the filter output, and u is the filter input.
In general the filter parameter a can be set directly. In this simulator Eq. 1 is developed by discretizing a continuous-time filter. The derivation is shown in detail in filter_algorithm.pdf. There it is shown that
a = h/(Tf + h) (Eq. 2)
For the filter given by Eq. 1 to be stable, a must be between 0 and 1.
Frequency response
The amplitude gain of the frequency response of a filter expresses how a sinusoid is attenuated through the filter. In the simulator the amplitude gain of the filter is plotted. The amplitude gain is calculated from the z-transfer function of Eq. 1. This transfer function found by taking the z-transform of Eq. 1, and it is
Hf(z) = Y(z)/U(z) = az/[z-(1-a)] (Eq. 3)
The amplitude gain is calculated as the absolute value of Hf(z) when z = ejwh where w is the frequency [rad/s] and h [s] is the sampling interval. j is the imaginary unit. In the simulator the Bode.vi function in LabVIEW is used to calculate and plot the amplitude gain in a Bode diagram.
The relation beween the time-constant Tf and the filter bandwidth fb [Hz] for Hf(z) is rather complicated. However, if the sampling time h is relatively small (less than 1/5 of Tf) the following relation holds (approximately):
fb [Hz] ~ 1/(2*pi*Tf) (Eq. 4)
How random noise is propagated through the filter
It is useful to know how the filter attenuates random noise. The attenuation can be expressed as the ratio between the standard deviation of the filter output and the standard deviation of the filter input, hence "standard deviation gain", Ksigma (sigma is the greek character symbol for standard deviation). In random_noise_attenuation.pdf it is shown that
Ksigma = sqrt(a/(2-a)) (Eq. 5)
where a is given by Eq. 2.
Tasks
- Manually adjusted input: The only input in this subtask is u3 (hence set the amplitude of the sinusoid to zero and the amplitude of the random noise to zero). Adjust u3 arbitrarily for various time-constants Tf. How does the relation between the output and the input (u3) depend on Tf? More specifically, is the filtering stronger or looser as Tf. is increased? In particalular, what is the relation between the output and the input signal if the input signal is constant?
- Sinusoidal input: Set u3 (manual
input) and u2 (random input) to zero. Set the amplitude of the sinusoid to 1
and the frequency to (say) 0.2 Hz.
- Observe how the amplitude attenuation through the filter depends (qualitatively) on Tf by looking at the simulated responses. Is this observation in accordance with the amplitude gain Bode?
- Set Tf to one specific value, say 0.5 s. The corresponding bandwidth fb [Hz] of the filter can be found by comparing the input and output signals. Find "experimentally" the bandwidth by adjusting the frequency of the input signal so that the amplitude of the output is 1/sqrt(2) = 71% of the amplitude of the input signal. Is this "experimental" bandwidth in accordance with the theoretical bandwidth as given by Eq. 4? Finally, is the experimental bandwidth in accordance with the bandwidth that you can fins from the Bode plot?
- Random input: Set u1 (sinusoid) and u2
(manual input) to zero. Set Tf to one specific value, say 0.5
s. Set the maximum random amplitude B to 1.
- Observe how the noise attenuation through the filter depends (qualitatively) on Tf by looking at the simulated responses. Is the filtering (the attenuation or smoothing) stronger with large Tf or with small Tf?
- Assume that you want to find Tf so that Ksigma is 0.2, i.e. the filter attenuates the noise 5 times (with respect to the standard deviations, as explained above). Find Tf experimentally so that Ksigma = 0.2. What is the theoretical Ksigma (it is caclulated and displayed on the simulator)? Are these Ksigma values very different?
- "Ideal" measurement signal plus random noise: Assume that the input to the filter consists of a sum an "ideal" measurement signal and random noise. Is there any drawback of having a filter with very strong filtering related to the transfer of the ideal measurement signal through the filter? Demonstrate your answer by a proper simulation!
Updated 2 September 2017. Developed by Finn Haugen. E-mail: finn@techteach.no.
